7  Inferential Statistics

Inferential Statistics, woh branch hai statistics ki jo data sets se conclusions nikalne, predictions karne, aur hypotheses test karne mein madad karti hai. Yeh method aksar chhote samples se liye gaye data par mabni hota hai, aur phir us data ke base par bade populations ke baare mein generalizations ya predictions kiye jaate hain.

7.1 Inferential Statistics Ke Main Components 🛠️

7.1.1 Dependent vs. Independent Variable

7.1.1.1 Dependent Variables 📉

Dependent Variables, ya Inhsar Karne Wale Muttahidat, woh variables hote hain jinki value ya status independent variable ke asar se badalti hai. Ye experiment ya study ke outcome ya result ko represent karte hain.

• Example: Usi school ki research mein, “class performance” dependent variable hai jo ke “neend ki miqdaar” se affect hota hai.

7.1.1.2 Independent Variables🌟

Independent Variables, ya Khud Mukhtar Muttahidat, woh variables hote hain jin ki value ya status khud se set hoti hai aur jinka asar dosre variables par hota hai. Ye research ya experiment mein woh factors hote hain jinhe researcher change karta hai ya control karta hai taake dekha ja sake ke unka asar dependent variable par kya hota hai.

• Example: Maan lijiye aap Karachi ke kisi school mein research kar rahe hain ke kitni neend students ko mil rahi hai aur iska unki class performance par kya asar hota hai. Yahan, “neend ki miqdaar” (hours of sleep) ek independent variable hai.

7.1.1.3 Independent aur Dependent Variables Ka Taluq 📈📉

In dono variables ka taluq research aur data analysis mein bohot ahem hota hai. Independent variable woh factor hai jise change kiya jata hai ya jo naturally vary hota hai, aur dependent variable woh outcome hai jise measure kiya jata hai. Inka sahi identification aur use se researchers aur scientists ye samajh sakte hain ke ek factor dusre par kaise asar daalta hai.

Example: Agar Lahore mein air quality ka study kiya ja raha hai aur dekha jaa raha hai ke iska asar logon ki health par kya hai, to “air quality” independent variable hoga aur “logon ki health” dependent variable. Yahaan ye dekha jayega ke air quality ke behtar ya bura hone se logon ki health kaise affected hoti hai. 📚🔬✨📉

Here’s a table comparing Dependent and Independent Variables:

Aspect	Independent Variable	Dependent Variable
Definition	Variable that is changed or controlled in a scientific experiment.	Variable being tested and measured in a scientific experiment.
Control in Experiments	Manipulated or selected by the researcher.	Observed and measured - changes in response to the independent variable.
Role in Analysis	Determines the conditions or groups in the study.	Outcome or result that is measured to see the effect of the independent variable.
Desi Example	Temperature levels in a study to see its effect on crop growth.	Crop growth in response to different temperature levels.

• The Independent Variable is the “Temperature levels”. This is what the researcher would change or control to observe the effects.
• The Dependent Variable is the “Crop growth”. This is what the researcher is measuring, and it’s expected to change in response to the different temperature levels.

7.1.2 Hypothesis Testing (Hypothesis Ka Imtehan):

• Yeh statistical analysis ka ek method hai jisme aapke data ko test kiya jaata hai.
• Kisi hypothesis ya assumption ko test karne ke liye use kiya jata hai.
• Example: Farz karein, aap ye test karna chahte hain ke Islamabad aur Lahore mein students ki science understanding mein koi significant farq hai ya nahi.

Aaiye baat karte hain “Hypothesis Testing” (Hypothesis Ka Imtehan) ke baare mein! 📊🔬

Hypothesis Testing, ek statistical method hai jo ke science aur data analysis mein use hota hai taake kisi specific assumption ya da’wa (hypothesis) ko test kiya ja sake. Is process mein, hum pehle ek hypothesis banate hain, phir data collect karte hain, aur uske baad statistical methods se ye dekhte hain ke kya humare collected data se wo hypothesis support hota hai ya nahi.

7.1.2.1 Hypothesis Testing Ke Steps 📐

1. Null Hypothesis (Null Hypothesis, H0): Yeh wo basic assumption hota hai jo kehti hai ke koi khaas effect ya farq nahi hai.
2. Alternative Hypothesis (Mutebadil Hypothesis, H1): Yeh hypothesis null hypothesis ke opposite hota hai, aur ye kehta hai ke koi effect ya farq hai.
3. Data Collection (Data Ikattha Karna): Relevant data collect karna jo hypothesis ko test karne ke liye zaroori ho.
4. Statistical Test (Shumariyati Test): Ek suitable statistical test perform karna taake data ko analyze kiya ja sake.
5. Result (Nateeja): Test ke results se conclusion nikalna ki kya null hypothesis ko reject karna chahiye ya nahi.

7.1.2.2 Hypothesis Testing Ki Misal 🌟

Example: Maan lijiye, aap ye test karna chahte hain ke Karachi aur Lahore mein students ki math skills mein koi significant difference hai ya nahi. Yahan, aapka null hypothesis \(H_0\) yeh hoga ke dono cities ke students ki skills mein koi farq nahi hai, aur alternative hypothesis \(H_1\) yeh hoga ke ek significant difference hai. Phir aap dono cities ke schools se data collect karte hain aur statistical test jaise t-test ya ANOVA perform karte hain taake dekha ja sake ke kya aapka data H0 ko reject karta hai ya nahi.

7.1.2.3 Hypothesis Testing Ki Importance 📈

Hypothesis testing research, science, aur business decisions mein bohot ahem hota hai. Yeh method humein yeh samajhne mein madad karta hai ke kya humare observations kisi real effect ki wajah se hain ya sirf chance ki wajah se. Is se hum informed decisions le sakte hain aur new theories ya products develop kar sakte hain.

Ye especially tab zaroori hota hai jab hume kisi assumption ko validate karna ho ya jab hum new discoveries ya insights ki talash mein hote hain. 📚🔬✨📉

7.1.2.4 Case Study for Hypothesis Testing-Health Drink Ka Asar 🥤💡

Situation: Aap ek nutritionist hain aur aapne recently ek naya health drink develop kiya hai. Aapka da’wa (claim) hai ke yeh drink regular istemal karne se logon ki overall health mein significant improvement hota hai.

7.1.2.4.1 Hypothesis Formulation 📝

1. Null Hypothesis \(H_0\): Health drink ka koi significant asar nahi hota hai logon ki health par.
2. Alternative Hypothesis \(H_1\): Health drink regular istemal karne se logon ki health mein significant improvement hota hai.

7.1.2.4.2 Data Collection and Experiment Setup 📊

• Aap Lahore ke ek group of volunteers ko choose karte hain aur unhe randomly do groups mein divide karte hain: Ek group ko aap naya health drink dete hain aur dusre group ko aam drink (placebo).
• Phir aap unke health parameters jaise blood pressure, energy levels, aur immune response ko measure karte hain start se pehle aur phir kuch weeks ke regular use ke baad.

7.1.2.4.3 Statistical Test and Analysis 📈

• Aap statistical tests jaise t-test ya ANOVA ka istemal karte hain taake compare kiya ja sake ke dono groups mein health parameters mein kya significant changes aaye hain.
• Test ke results se pata chalta hai ke health drink wale group mein significant improvements hain compare karte hue placebo group se.

7.1.2.4.4 Result and Conclusion 🌟

• Agar test ke results significant hote hain, toh aap H0 ko reject kar sakte hain aur conclude kar sakte hain ke health drink ka asal mein significant positive asar hota hai health par.
• Agar results significant nahi hote, toh aap H0 ko reject nahi kar sakte aur conclude karte hain ke drink ka koi special asar nahi hai.

7.1.2.5 Importance of This Test 📌

Yeh hypothesis testing ka example real-world mein product testing aur research mein kaise important role ada karta hai dikhata hai. Yeh method se aap product ke claims ko scientifically validate kar sakte hain, jo ke consumers aur regulatory bodies ke liye confidence build karta hai. Aise tests se aapko valuable insights milte hain jo aapke product development aur marketing strategies ko guide karte hain. 🥤🔍✨📚

7.2 Confidence Intervals:

• Yeh range batati hai jisme aapke true population parameter hone ki probability hoti hai.
• Example: Agar aap Karachi mein ek survey conduct karte hain aur pata lagate hain ke average monthly household income ki confidence interval kya hai. Bilkul, aaiye baat karte hain “Confidence Interval” (Yaqeen Ke Waqfay) ke baare mein, Roman Urdu aur emojis ke saath! 📊📈

Confidence Interval (CI), ya Yaqeen Ke Waqfay, ek statistical term hai jo describe karta hai ke ek certain range mein, with a specific probability (confidence level), asal population parameter ki value kahaan gir sakti hai. Ye basically ek estimate hai ke aapke sample data se nikale gaye result kitne accurate hain jab unhe poore population par apply kiya jaye.

7.2.1 Confidence Interval Ka Structure 📐

• Upper and Lower Bounds: CI mein usually ek lower bound aur ek upper bound hota hai, jo ke yeh batate hain ke aapke estimated parameter ki asal value kis range mein ho sakti hai.
• Confidence Level: Commonly, 95% confidence level istemal kiya jata hai, lekin ye 90%, 99%, ya kisi aur level ka bhi ho sakta hai. Ye level batata hai ke kitni bar, agar hum bohot saare samples lein, to asal value is interval mein gir sakti hai.

Example: Maan lijiye aapne Lahore ke ek college mein students ka average test score calculate kiya hai. Aapka sample mean 70 hai aur aapne 95% confidence interval calculate kiya hai jo 68 se 72 ke beech hai. Iska matlab ye hai ke aap 95% sure hain ke poore college ke students ka average score is range mein hoga.

7.2.2 Confidence Interval Ka Importance 📌

1. Data Ki Accuracy Ka Andaza: Ye aapko batata hai ke aapke sample se nikale gaye estimates kitne reliable hain.
2. Research Mein: Scientific research mein, CI ka use often results ko present karne ke liye kiya jata hai taake readers ko yeh pata chale ke findings kitne sure hain.
3. Business Decisions: Business mein, CI ka istemal market research aur financial forecasting mein hota hai taake risk aur uncertainty ko quantify kiya ja sake.
4. Policy Making: Governments aur policymakers CI ka use kar sakte hain taake samajh sakein ke unke decisions kitne accurate hain based on the data available to them.

CI ek powerful statistical tool hai jo complex data ko samajhne aur us par based decisions lene mein key role ada karta hai. Ye especially tab zaroori hota hai jab hume data ke precision aur reliability ko quantify karna ho. 📚🔍✨📉

The equation for calculating a Confidence Interval (CI) typically revolves around the standard error of the mean and a multiplier derived from the desired confidence level. For a simple CI around a sample mean, the equation is:

\[\text{CI} = \bar{x} \pm (Z \times \text{SE})\]

Where: - \(\bar{x}\) is the sample mean. - \(Z\) is the Z-score corresponding to the desired confidence level (for example, 1.96 for a 95% confidence interval). - \(\text{SE}\) is the standard error of the sample mean.

Standard Error (SE) Equation:

The standard error of the sample mean is calculated as:

\[\text{SE} = \frac{s}{\sqrt{n}}\]

Where: - \(s\) is the sample standard deviation. - \(n\) is the sample size.

7.2.3 Putting It All Together:

For a 95% confidence interval, the Z-score is approximately 1.96. So, if your sample mean is 50, the sample standard deviation is 10, and your sample size is 100, the confidence interval would be calculated as:

1. Calculate the standard error: \(\text{SE} = \frac{10}{\sqrt{100}} = 1\).
2. Multiply by the Z-score: \(1.96 \times 1 = 1.96\).
3. Apply to the sample mean: \(50 \pm 1.96\), which gives you an interval of \(48.04\) to \(51.96\).

This means you can be 95% confident that the true population mean lies between 48.04 and 51.96. Remember, the confidence interval width can be influenced by both the variability in the data (as captured by the standard deviation) and the size of the sample, with larger samples typically yielding narrower intervals.

7.3 P-value (P-Value) 📊

P Value, statistics mein ek ahem concept hai jo hypothesis testing mein istemal hota hai.

• Tafseel: P value woh probability hoti hai ke test ke results itne extreme ho jaise ke actual mein dekhe gaye, agar humara null hypothesis (basic assumption) sahi ho. Ye basically batata hai ke kisi given dataset par jab aik statistical model apply kiya jata hai, to observed results kitne unusual hain.
• Ahmiyat: P value ki madad se, researchers ye tay kar sakte hain ke unke results kisi real effect ki wajah se hain ya sirf ittefaq. 🎲🔬
• Low vs High P Value:
  • Low P Value (Kam P Qiymat): Iska matlab hai ke observed results shayad ittefaq nahi hain aur koi asal effect ho sakta hai. Aksar, P value 0.05 (5%) se kam hone par, hum null hypothesis ko reject karte hain.
  • High P Value (Zyada P Qiymat): Iska matlab hai ke observed results ittefaq se ho sakte hain aur koi significant effect nahi hai. 📈📉

7.3.1 P-value threshold

P-value threshold, woh point hota hai jis par faisla kiya jata hai ke kya humare natije significant hain ya nahi.

• Tafseel: Jab aap koi hypothesis test karte hain, to aap pehle ye decide karte hain ke kis level par aap results ko significant samjhenge. Yehi level aapka P-value threshold hai. 🚦🔍
• Common Threshold: Aksar, scientists aur researchers 0.05 (ya 5%) ko as a standard threshold choose karte hain. Iska matlab hai ke agar P-value 0.05 se kam ho, to hum samajhte hain ke results statistically significant hain. 💡📈
• Kaise Set Karein:
  • Research Context ko Samjhein: Threshold set karne se pehle, aapko apne research ke context ko samajhna zaroori hai. Kuch studies mein zyada strict threshold (jaise 0.01) zaroori hota hai, khaas kar jahan results ka serious implications ho sakta hai.
  • Risk ko Madde Nazar Rakhein: Lower threshold se aap Type I error (false positive) ka risk kam karte hain, lekin is se Type II error (false negative) ka risk badh sakta hai. Is liye, balance important hai. ⚖️🔬
  • Field ke Standards: Different fields ke different standards hote hain. Medical research mein shayad zyada strict standards hote hain as compared to social sciences. Is liye, apne field ke norms aur past studies ko bhi dekhein. 🧪📚

7.3.1.1 Ahmiyat (Importance) 🌟

P-value threshold set karna research design ka aham hissa hota hai kyun ke yeh aapke results ki interpretation ko directly affect karta hai. Sahi threshold set kar ke, aap more reliable aur accurate conclusions tak pahunch sakte hain. 🎯📊

p-value threshold

Setting the P-value threshold is a fundamental part of hypothesis testing, ensuring that the conclusions drawn from a study are based on sound statistical reasoning. The choice of threshold depends on the specific context of the research, the inherent risks of making errors, and the standards of the particular field of study.

7.3.2 Alpha \(\alpha\) and P-value

Alpha \(\alpha\), statistics mein hypothesis testing ke context mein istemal hota hai aur isay significance level bhi kaha jata hai.

Alpha ko hum usually 0.05 (ya 5%) par set karte hain, lekin ye research ke context aur zarurat ke mutabiq vary ho sakta hai. Ye basically ek threshold hota hai jis par hum decide karte hain ke koi finding statistically significant hai ya nahi.

Alpha ko \(\alpha\) se denote kiya jata hai aur ye probability hoti hai ke hum null hypothesis ko false positive taur par reject kar dein. Iska matlab hai ke agar aapka alpha 0.05 hai, to aap 5% tak acceptable samajhte hain ke aap galat taur par null hypothesis ko reject kar dein.

• Tafseel: Alpha woh probability hoti hai jis par hum decide karte hain ke koi finding statistically significant hai ya nahi. Ye basically Type I error (false positive) ki probability ko represent karta hai - yani ke, hum kitni probability tak acceptable samajhte hain ke hum galat taur par null hypothesis ko reject kar dein. 🎲🚫
• Common Value: Aksar, alpha ko 0.05 (ya 5%) par set kiya jata hai, lekin ye research ke context aur zarurat ke mutabiq vary ho sakta hai. 💡🔍

7.3.2.1 Alpha aur P-value ka Rishta (Alpha and P-value’s Link) 🔗📈

Alpha aur P-value aapas mein closely linked hote hain aur hypothesis testing mein unka ek sath istemal hota hai.

• Comparison: Jab aap hypothesis test karte hain, to aap jo P-value calculate karte hain, usay apne set kiye gaye alpha se compare karte hain. Agar P-value alpha se kam hota hai, to hum null hypothesis ko reject karte hain aur conclude karte hain ke result statistically significant hai. 📊✅
• Example: Agar aapka alpha 0.05 hai aur aapka P-value 0.03 aata hai, to iska matlab hai ke aapke results ka statistical significance alpha level se zyada hai, aur aap null hypothesis ko reject kar sakte hain. 🔍📉
• Balance in Decision Making: Alpha ki value ka careful selection zaroori hai kyun ke ye Type I error (false positive) aur Type II error (false negative) ke risk ko balance karta hai. 🧐⚖️

7.3.2.2 Ahmiyat (Importance) 🌟

Alpha aur P-value ka sahi istemal aur unka aapas mein rishta samajhna research mein bohot ahem hota hai. Ye dono values mil kar help karti hain ke hum research ke results ko kis tarah interpret karein aur kitne confidence ke sath kisi conclusion tak pahunch sakte hain. 🎯🔬

alpha and p-value

Alpha \(\alpha\) aur P-value dono hypothesis testing ke critical elements hain. Alpha aapke research ke risk tolerance ko set karta hai, jabke P-value aapke data se milne wale evidence ki strength ko measure karta hai. In dono ka sahi use aur samajh research mein robust aur credible conclusions tak pahunchne mein madad karta hai.

7.4 Statistical Tests

Which statistical test to use depends on the type of data you have and the research question you want to answer. The following flowchart will help you choose the right statistical test for your data.

7.4.1 Types of Statistical Tests

Parametric vs. Non-Parametric Tests are the two main types of statistical tests. Parametric tests assume that the data is normally distributed, whereas non-parametric tests do not make this assumption. The following flowchart will help you choose the right statistical test for your data.

graph TD
    A[Statistical Tests] --> B[Categorical Data]
    A --> C[Numerical Data]
    B --> D[Chi-Square Test]
    C --> E[Normally Ditributed Data]
    C --> F[Data is Homogenious]
    D --> G[One Sample Chi-Square Test]
    D --> H[Two Samples Chi-Square Test]
    E --yes--> I(Parametric Tests)
    F --yes--> I(Parametric Tests)
    E --no--> J(Non-Parametric Tests)

7.4.2 Z-test vs. t-test

Choosing between a Z-test and a T-test for hypothesis testing depends primarily on two factors: the sample size and whether the population standard deviation is known.

7.4.2.1 Z-test:

1. When to Use:
   • The population standard deviation is known.
   • The sample size is large (commonly, n ≥ 30). With large samples, the sample standard deviation approximates the population standard deviation.
   • For proportions (e.g., testing the proportion of success in a sample against a known population proportion).
2. Characteristics:
   • Based on the Z-distribution, which is a normal distribution as n becomes large.
   • More commonly used in quality control and standardization processes.

7.4.2.2 T-test:

1. When to Use:
   • The population standard deviation is unknown.
   • The sample size is small (typically, n < 30).
   • Suitable for cases where the data is approximately normally distributed, especially in small samples.
2. Characteristics:
   • Based on the T-distribution, which accounts for the additional uncertainty due to the estimation of the population standard deviation from the sample.
   • T-distribution becomes closer to the normal distribution as the sample size increases.

7.4.2.3 General Guidelines:

• Large Samples: With large sample sizes, the T-test and Z-test will give similar results. This is because the T-distribution approaches the normal distribution as the sample size increases.
• Small Samples: When the sample size is small and the population standard deviation is unknown, the T-test is generally the appropriate choice due to its ability to account for the uncertainty in the standard deviation estimate.
• Unknown Population Standard Deviation: Even with large samples, if the population standard deviation is unknown and cannot be reliably estimated, a T-test is usually preferred.

7.4.2.4 Conclusion:

• Use the Z-test for large sample sizes or when the population standard deviation is known.
• Use the T-test for small sample sizes or when the population standard deviation is unknown.

In practice, the T-test is more commonly used in many research scenarios due to the rarity of knowing the population standard deviation and often dealing with smaller sample sizes.

7.4.3 Parametric Tests

Parametric tests are used when the data follows a normal distribution. The following flowchart will help you choose the right parametric test for your data.

Which test to choose from t-test and z-test? The following flowchart will help you.

graph TD
   A[Parametric Tests] --> B[One Variable]
   A --> C[Two Variables]
   B --> D[Is sample size less than 30?]
   C --> D
   D --Yes--> E[t-test]
   D --No--> F[Is population standard deviation known?]
   F --Yes--> G[z-test]
   F --No--> E

The following flowchart will help you choose the right parametric test for your data.

graph LR
   A[Parametric Tests] --> B[One Variable]
   A --> C[Two Variables]
   A --> D[Three or more Variables]
   A --> Da[Two Continuous Dependent variables]
   Da --> Db[Correlation]
   Db --> Dc[Pearson's Correlation Coefficient]
   B --> E(One Sample t-test/z-test)
   C --> F(Independent Samples)
   D --> Ja[Only one Continuous Dependent variable]
   D --> Jb[Two or more Continuous Dependent variables]
   Ja --> H[One Factor]
   Ja --> I[Two Factors]
   Ja --> J[Three or more Factors]
   H --> K[One-Way ANOVA]
   I --> L[Two-Way ANOVA]
   J --> M[Three or N-Way ANOVA]
   Jb --> N[MANOVA Multivariate Analysis of Variance]

7.4.4 Non-parametric Tests

Non-parametric tests are used when the data does not follow a normal distribution. The following flowchart will help you choose the right non-parametric test for your data.

graph LR
    A[Non-Parametric Tests] --> B[One Variable]
    A --> C[Two Variables]
    B --> D[Compares one Continuous Dependent Variable to a fixed value]
    B --> E[Compares Two Paird samples]
    D --> F[Wilcoxon Signed Rank Test]
    E --> F
    C --> H[Compares Two Independent samples]
    H --> I[Mann-Whitney U Test]
    A --> J[Three or more Independent samples]
    J --> K[Kruskal-Wallis Test] --> L[Compares three or more median ranks, 1 variable] --> M[Kruskal-Wallis Test]
    J --> N[Compares three or more median ranks, 2 variables] --> O[Freidman Test]
   

Now we will see how to perform these tests in Python.

7.4.5 Chi-Square Test (Chi-Square Test) 📊

Chi-Square Test, categorical data ko analyze karne ke liye use hota hai. We can also call it Chi-squred test of independence. Is test mein, hum dekhte hain ke kya observed frequencies aur expected frequencies mein koi significant difference hai ya nahi.

7.4.5.1 Assumptions of Chi-Square Test

The assumptions of the Chi-Squared test are:

1. The variables under study are categorical (nominal or ordinal) variables.
2. The observations are independent of each other. This means that the occurrence of an outcome does not affect the other outcomes.
3. The data should be frequency counts of categories and not percentages or transformed data.
4. Each observed frequency, O_i, and expected frequency, E_i, should be greater than 5. If this assumption is violated, then the results might not be valid.
5. These assumptions need to be met for the Chi-Squared test to be valid.

7.4.5.2 Chi-suqare Test in Python

To perform a Chi-Squared test on the Titanic dataset in Python, we can use the scipy.stats library. The Chi-Squared test is often used to determine whether there is a significant association between two categorical variables. In this example, let’s test whether there is a significant association between the ‘Sex’ (male or female) and ‘Survived’ (0 = No, 1 = Yes) variables in the Titanic dataset.

Null Hypothesis \(H_0\): There is no significant association between gender (‘Sex’) and survival (‘Survived’) on the Titanic. This means any observed differences in survival rates between genders in the dataset are due to chance and not due to an underlying relationship.

Alternative Hypothesis \(H_1\): There is a significant association between gender (‘Sex’) and survival (‘Survived’) on the Titanic. This implies that the differences in survival rates are not just due to chance but are influenced by the passengers’ gender.

In hypothesis testing, the null hypothesis is what we attempt to disprove using our data. If the p-value from the Chi-Squared test is less than a certain threshold (commonly 0.05), we reject the null hypothesis in favor of the alternative hypothesis, concluding that there is indeed a statistically significant association between the two variables. If the p-value is greater than the threshold, we fail to reject the null hypothesis, meaning we do not have enough evidence to claim a significant association.

import pandas as pd
import numpy as np
import seaborn as sns
from scipy.stats import chi2_contingency

# Load the dataset
titanic = sns.load_dataset('titanic')

# Create a contingency table
contingency_table = pd.crosstab(titanic['sex'], titanic['survived'])

# Perform the Chi-Squared test
chi2, p, dof, expected = chi2_contingency(contingency_table)

# Display the results
print(f"Chi-Squared Value: {chi2}")
print(f"P-value: {p}")
print(f"Degrees of Freedom: {dof}")
print(f"Expected Frequencies:\n {expected}")
print("-------------------------------------")
# print the results based on if else condition
if p < 0.05:
    print("Reject the null hypothesis, as there is a significant association between the variables.")
else:
    print("Fail to reject the null hypothesis, as there is no significant association between the variables.")

Chi-Squared Value: 260.71702016732104
P-value: 1.1973570627755645e-58
Degrees of Freedom: 1
Expected Frequencies:
 [[193.47474747 120.52525253]
 [355.52525253 221.47474747]]
-------------------------------------
Reject the null hypothesis, as there is a significant association between the variables.

7.4.5.3 Explanation:

1. Load Dataset: We use Seaborn’s built-in function to load the Titanic dataset.
2. Create Contingency Table: We create a contingency table (or cross-tabulation) between ‘Sex’ and ‘Survived’ using Pandas.
3. Chi-Squared Test: We use chi2_contingency from scipy.stats to perform the Chi-Squared test. This function returns the Chi-Squared value, the p-value, the degrees of freedom, and the expected frequencies if there was no association between the variables.
4. Results: The results are printed out. The p-value is used to determine the statistical significance. Typically, a p-value less than 0.05 indicates a statistically significant association between the variables.

As the p_value in this test is P-value: 1.1973570627755645e-58, we reject the null hypothesis.

7.4.5.4 Calculating Chi-Squared Manually

The Chi-Squared test statistic is calculated using the following formula:

\[\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}\]

Where:

• \(\chi^2\) is the Chi-Squared statistic.
• \(O_i\) is the observed frequency.
• \(E_i\) is the expected frequency.
• The summation \(\sum\) is over all categories.

The expected frequency is calculated as:

\[E_i = \frac{(row \ total) \times (column \ total)}{grand \ total}\]

The Chi-Squared test compares the observed frequencies in each category of a contingency table with the frequencies expected under the null hypothesis, which is that the variables are independent.

7.4.6 t-test (t-test) 📊

T-test, numerical data ko analyze karne ke liye use hota hai. Is test mein, hum dekhte hain ke kya observed means aur expected means mein koi significant difference hai ya nahi.

7.4.6.1 Assumptions of t-test

1. Normality: Data ka distribution normal hona chahiye.
2. Independence: Data points independent hona chahiye.
3. Randomness: Data points random hona chahiye.
4. Sample Size: Sample size chhota hona chahiye (n < 30).
5. Scale: Data ka scale interval ya ratio hona chahiye.
6. Outliers: Data mein outliers nahi hona chahiye.
7. Linearity: Data ka relationship linear hona chahiye.
8. Homoscedasticity: Data ka variance same hona chahiye.

7.4.6.2 Types of t-test

graph LR
A[t-test] --> B[One Sample t-test]
A[t-test] --> C[Two Samples t-test]
C --> D[Independent Samples t-test]
C --> E[Paired Samples t-test]

1. One Sample T-test: Is test mein, hum dekhte hain ke kya aik sample ka mean kisi specific value se different hai ya nahi.
2. Independent Samples T-test: Is test mein, hum dekhte hain ke kya do samples ke means mein koi significant difference hai ya nahi.
3. Paired Samples T-test: Is test mein, hum dekhte hain ke kya do samples ke means mein koi significant difference hai ya nahi, jab ke wo samples related hain.

7.4.6.3 One Sample T-test

One Sample T-test, aik sample ka mean kisi specific value se different hone ki probability ko test karta hai. Is test mein, hum dekhte hain ke kya aik sample ka mean kisi specific value se different hai ya nahi.

# Import the required libraries
import numpy as np
from scipy.stats import ttest_1samp

# Create a sample data
ages = np.array([32, 34, 29, 29, 22, 39, 38, 37, 38, 36, 30, 26, 22, 22])

mu = 30 # mean of the population

# Perform the one-sample t-test
t_statistic, p_value = ttest_1samp(ages, mu)

# Print the results
print(f"t-statistic: {t_statistic}")
print(f"p-value: {p_value}")
print("-------------------------------------")
# print the results based on if else condition
if p_value < 0.05:
    print("Reject the null hypothesis,\n as the sample mean is significantly different from the population mean.")
else:
    print("Fail to reject the null hypothesis,\n as the sample mean is not significantly different from the population mean.")

t-statistic: 0.5973799001456603
p-value: 0.5605155888171379
-------------------------------------
Fail to reject the null hypothesis,
 as the sample mean is not significantly different from the population mean.

Try to change the value of mu and see how the results change. and if it becomes significantly different or not.

7.4.6.4 Two Samples t-test

7.4.6.4.1 Independent Samples t-test

Independent Samples t-test, do independent samples ke means mein koi significant difference hone ki probability ko test karta hai. Is test mein, hum dekhte hain ke kya do samples ke means mein koi significant difference hai ya nahi.

# Import the required libraries
import numpy as np
from scipy.stats import ttest_ind

# Create two sample data
ages1 = np.array([32, 34, 29, 29, 22, 39, 38, 37, 38, 36, 30, 26, 22, 22])
ages2 = np.array([27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34])


# Perform the two-sample t-test
t_statistic, p_value = ttest_ind(ages1, ages2)

# Print the results
print(f"t-statistic: {t_statistic}")
print(f"p-value: {p_value}")

# print the results based on if else condition
if p_value < 0.05:
    print("Reject the null hypothesis,\n as the sample means are significantly different.")
else:
    print("Fail to reject the null hypothesis,\n as the sample means are not significantly different.")

t-statistic: 2.0979439363492083
p-value: 0.04577767375684831
Reject the null hypothesis,
 as the sample means are significantly different.

7.4.6.4.2 Paired Samples t-test

Paired Samples t-test, do related samples ke means mein koi significant difference hone ki probability ko test karta hai. Is test mein, hum dekhte hain ke kya do samples ke means mein koi significant difference hai ya nahi, jab ke wo samples related hain.

# Import the required libraries
import numpy as np
from scipy.stats import ttest_rel

# Create two sample data before and after
before = np.array([32, 34, 29, 29, 22, 39, 38, 37, 38, 36, 30, 26, 22, 22])
after = np.array([27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34])

# Perform the paired t-test
t_statistic, p_value = ttest_rel(before, after)

# Print the results
print(f"t-statistic: {t_statistic}")
print(f"p-value: {p_value}")

# print the results based on if else condition
if p_value < 0.05:
   print("Reject the null hypothesis,\n as the before mean is significantly different to the after mean.")
else:
   print("Fail to reject the null hypothesis,\n as the before mean is not significantly different to the after mean.")

t-statistic: 1.8116836198069448
p-value: 0.0931902262006994
Fail to reject the null hypothesis,
 as the before mean is not significantly different to the after mean.

7.4.6.5 Role of Variance in t-test

Variance, data points ke spread ko measure karta hai.

• Low Variance: Data points close honge mean ke.
• High Variance: Data points far honge mean se.

Variance ka role t-test mein:

• Independent Samples t-test: Is test mein, hum dekhte hain ke do samples ke means mein koi significant difference hai ya nahi. Is test mein, agar dono samples ka variance same hoga, to hum ttest_ind use karenge, aur agar dono samples ka variance different hoga, to hum ttest_ind with unequal variance use karenge.

ttest_ind with unequal variance:

# Step-1: Import libraries
import numpy as np
from scipy.stats import ttest_ind

# Step 2: Create two datasets with unequal variance
np.random.seed(0)  # for reproducibility

# Create a dataset 'ages1' with mean=30, standard deviation=3, size=100
ages1 = np.random.normal(30, 3, 100)

# Create a dataset 'ages2' with mean=30, standard deviation=10, size=100
ages2 = np.random.normal(30, 10, 100)


# Perform the two-sample t-test
t_statistic, p_value = ttest_ind(ages1, ages2, equal_var=False)

# Print the results
print(f"t-statistic: {t_statistic}")
print(f"p-value: {p_value}")

# print the results based on if else condition
if p_value < 0.05:
    print("Reject the null hypothesis,\n as the sample means are significantly different.")
else:
    print("Fail to reject the null hypothesis,\n as the sample means are not significantly different.")

t-statistic: -0.5913989290785231
p-value: 0.5554059984405396
Fail to reject the null hypothesis,
 as the sample means are not significantly different.

When to use which test from t-test of z-test?

graph TD
   A[Is sample size > 30?]
   A --Yes--> B[Z-test]
   A --No--> C[Is population standard deviation known?]
   C --Yes--> B
   C --No--> D[T-test]

7.4.7 Z-test

Z Test, statistics mein istemal hone wala ek tareeqa hai jise hum population ke mean (ausat) ke bare mein hypotheses test karne ke liye use karte hain.

• Tafseel: Z Test tab istemal hota hai jab population ka standard deviation (maiyar-i-inhiraf) maloom ho aur sample size kafi bada ho (usually 30 se zyada). Is test mein, normal distribution ka istemal hota hai. 📏🔢
• Formula: Z Test ka formula hai: \[Z = \frac{(\text{sample mean} - \text{population mean})}{\text{standard deviation} / \sqrt{\text{sample size}}}\]
• Application: Ye test aksar business, psychology, aur medical research mein istemal hota hai jahan large data sets hoti hain. 🏥📚

7.4.7.1 Z Test ke Iqsaam (Types of Z Test) 🎲🔍

Z Test ke mukhtalif iqsaam hote hain jo mukhtalif scenarios aur zaruraton ke mutabiq use kiye jate hain.

1. One-Sample Z Test (Yek Namuna Z Imtehaan):
   • Istemaal: Jab ek sample ke mean ko kisi maloom population mean ke sath compare kiya jata hai.
   • Misal: Company ye test kar sakti hai ke unka naya product kya average sale time se zyada ya kam time mein bik raha hai.
2. Two-Sample Z Test (Do Namunon ka Z Imtehaan):
   • Istemaal: Do alag samples ke means ko aapas mein compare karna.
   • Misal: Do different factories ke production times ko compare karna ke kon si factory zyada efficient hai.
3. Z Test for Proportions (Tanasub ke Liye Z Imtehaan):
   • Istemaal: Population ke kisi hisse (proportion) ke bare mein hypotheses test karna.
   • Misal: Kisi election mein aik political party ke votes ke tanasub ka analysis.

7.4.7.2 Ahmiyat (Importance) 🌟

Z Test ki significance is mein hai ke ye large samples ke sath precise aur reliable results provide karta hai, khaas kar jahan population parameters maloom hon. Ye test researchers ko enable karta hai ke wo data ke patterns ko samajhne aur informed decisions lene mein madad le sakte hain. 📊💡

Z Test aur uske mukhtalif types, statistics aur data analysis mein widely istemal hote hain. Ye tests various scenarios mein data ko analyze karne ke liye aik powerful tool sabit hote hain, khaas taur par large datasets ke sath.

7.4.7.3 Z Test in Python

# Step-1: Import libraries
import numpy as np
from statsmodels.stats import weightstats as stests

# Step-2: Create a sample data
ages = np.array([32, 34, 29, 29, 22, 39, 38, 37, 38, 36, 30, 26, 22, 22, 27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34, 27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34])

# Step-3: Perform the Z-test
z_statistic, p_value = stests.ztest(ages, value=30, alternative='two-sided')

# Step-4: Print the results
print(f"z-statistic: {z_statistic}")
print(f"p-value: {p_value}")

# print the results based on if else condition
if p_value < 0.05:
    print("Reject the null hypothesis,\n as the sample mean is significantly different from the population mean.")
else:
    print("Fail to reject the null hypothesis,\n as the sample mean is not significantly different from the population mean.")

z-statistic: -2.2355502631512842
p-value: 0.025381245676198847
Reject the null hypothesis,
 as the sample mean is significantly different from the population mean.

Two Sample Z Test:

# Step-1: Import libraries
import numpy as np
from statsmodels.stats import weightstats as stests

# Step-2: Create two sample data with more than 30 samples and known population standard deviation
ages1 = np.array([32, 34, 29, 29, 22, 39, 38, 37, 38, 36, 30, 26, 22, 22, 27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34, 27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34])
ages2 = np.array([27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34, 27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34, 27, 29, 21, 20, 25, 24, 24, 26, 27, 28, 29, 30, 32, 34])

# Step-3: Perform the Z-test
z_statistic, p_value = stests.ztest(ages1, ages2, value=0, alternative='two-sided')

# Step-4: Print the results
print(f"z-statistic: {z_statistic}")
print(f"p-value: {p_value}")

# print the results based on if else condition
if p_value < 0.05:
    print("Reject the null hypothesis,\n as the sample means are significantly different.")
else:
    print("Fail to reject the null hypothesis,\n as the sample means are not significantly different.")

z-statistic: 1.4028075294672642
p-value: 0.1606742411215759
Fail to reject the null hypothesis,
 as the sample means are not significantly different.

7.4.8 ANOVA (Analysis of Variance) 📊

ANOVA, statistics mein istemal hone wala aik test hai jo multiple groups ke means mein koi significant difference hone ki probability ko test karta hai.

• Tafseel: ANOVA, multiple groups ke means mein koi significant difference hone ki probability ko test karta hai. Is test mein, hum dekhte hain ke kya do ya zyada groups ke means mein koi significant difference hai ya nahi. 📊🔍
• Types of ANOVA: ANOVA ke mukhtalif types hote hain jin mein se sab se common hai One-Way ANOVA. Is ke ilawa, Two-Way ANOVA, Three-Way ANOVA, aur MANOVA bhi istemal hote hain. 📊🔍
• One-Way ANOVA: Is test mein, hum dekhte hain ke kya do ya zyada groups ke means mein koi significant difference hai ya nahi. 📊🔍
• Two-Way ANOVA: Is test mein, hum dekhte hain ke kya do ya zyada groups ke means mein koi significant difference hai ya nahi, jab ke wo groups related hain. 📊🔍
• N-Way ANOVA: Is test mein, hum dekhte hain ke kya do ya zyada groups ke means mein koi significant difference hai ya nahi, jab ke wo groups related hain aur un groups mein aik categorical variable aur do continuous variables hain. 📊🔍
• MANOVA: Is test mein, hum dekhte hain ke kya do ya zyada groups ke means mein koi significant difference hai ya nahi, jab ke wo groups related hain aur un groups mein aik categorical variable aur do ya zyada continuous variables hain. 📊🔍

7.4.8.1 ANOVA ke Assumptions

ANOVA ke assumptions ye hain: 1. Normality: Data ka distribution normal hona chahiye. 2. Independence: Data points independent hona chahiye. 3. Homogeneity of Variance: Data ka variance same hona chahiye. 4. Randomness: Data points random hona chahiye.

7.4.8.2 One-Way ANOVA in Python

One-way ANOVA is used to compare two or more groups of samples across one continuous independent variable.

For example, you could use a one-way ANOVA to compare the height of people living in different cities.

import scipy.stats as stats

# Sample data: Growth of plants with three types of fertilizers
fertilizer1 = [20, 22, 19, 24, 25]
fertilizer2 = [28, 30, 27, 26, 29]
fertilizer3 = [18, 20, 22, 19, 24]

# Perform the one-way ANOVA
f_stat, p_val = stats.f_oneway(fertilizer1, fertilizer2, fertilizer3)

print("F-statistic:", f_stat)
print("p-value:", p_val)

# print the results based on if the p-value is less than 0.05

if p_val < 0.05:
    print(f"Reject null hypothesis: The means are not equal, as the p-value: {p_val} is less than 0.05")
else:
    print(f"Accept null hypothesis: The means are equal, as the p-value: {p_val} is greater than 0.05")

F-statistic: 15.662162162162158
p-value: 0.0004515404760997283
Reject null hypothesis: The means are not equal, as the p-value: 0.0004515404760997283 is less than 0.05

One-way ANOVA can also be done using StatsModels.

# One-way ANOVA using statsmodels
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

# Create a dataframe
# Sample data: Growth of plants with three types of fertilizers
fertilizer1 = [20, 22, 19, 24, 25]
fertilizer2 = [28, 30, 27, 26, 29]
fertilizer3 = [18, 20, 22, 19, 24]

df = pd.DataFrame({"fertilizer": ["fertilizer1"] * 5 + ["fertilizer2"] * 5 + ["fertilizer3"] * 5,
                   "growth": fertilizer1 + fertilizer2 + fertilizer3})

# Fit the model
model = ols("growth ~ fertilizer", data=df).fit()

# Perform ANOVA and print the summary table
anova_table = sm.stats.anova_lm(model, typ=2)
print(anova_table)

# print the results based on if the p-value is less than 0.05
if anova_table["PR(>F)"][0] < 0.05:
    print(f"Reject null hypothesis: The means are not equal, as the p-value is less than 0.05")
else:
    print(f"Accept null hypothesis: The means are equal, as the p-value is greater than 0.05")

                sum_sq    df          F    PR(>F)
fertilizer  154.533333   2.0  15.662162  0.000452
Residual     59.200000  12.0        NaN       NaN
Reject null hypothesis: The means are not equal, as the p-value is less than 0.05

/var/folders/4q/h5d6slgx2rs_drdwcmgf_htm0000gp/T/ipykernel_49854/3008466380.py:23: FutureWarning:

Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`

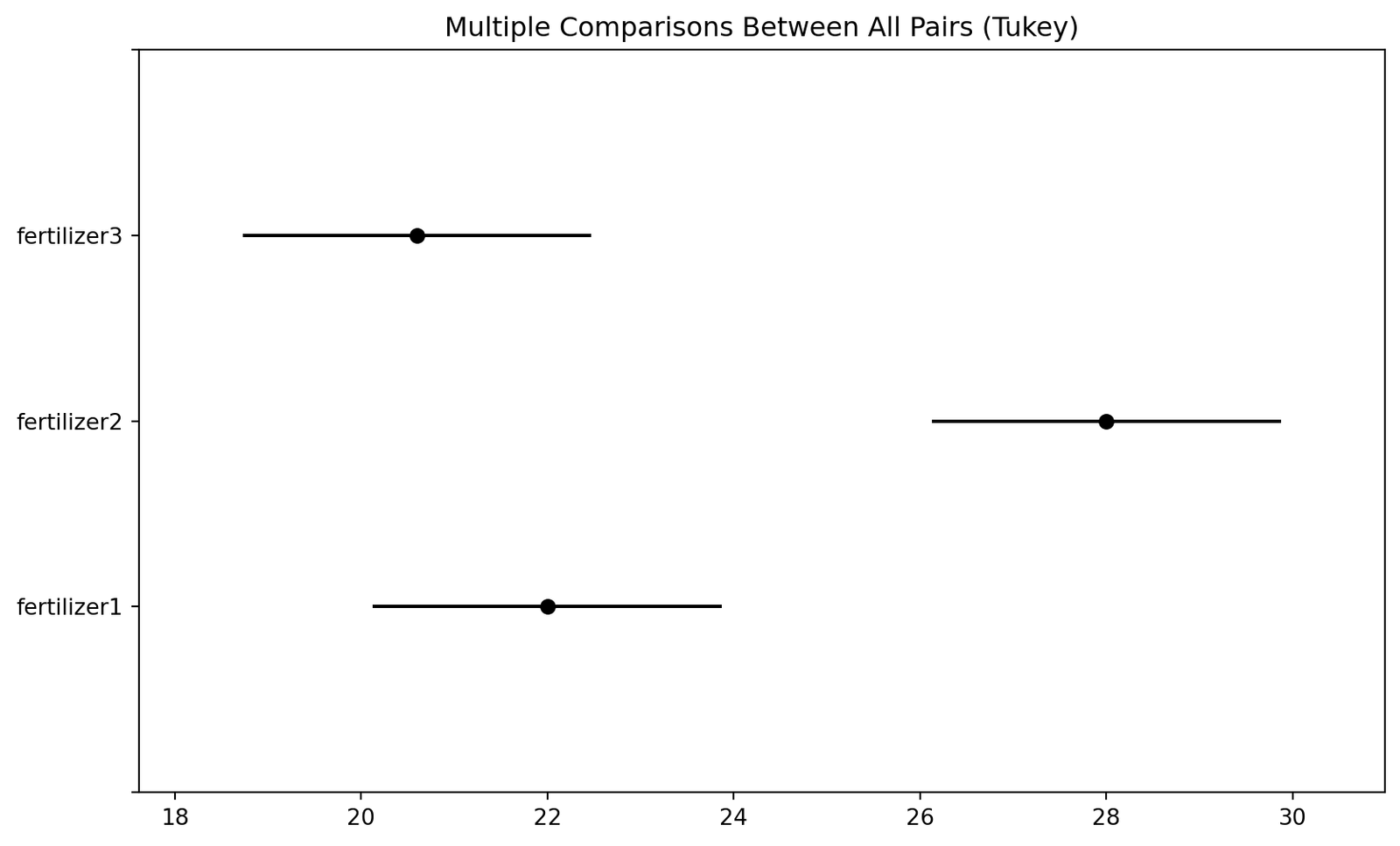
Based on the p-value, we can conclude that the means are not equal. In other words, the growth of plants is significantly different for the three types of fertilizers. We need to perform a post-hoc test to determine which fertilizers are significantly different from each other.

7.4.8.2.1 Post-Hoc Test for One-Way ANOVA

We will perform a post-hoc test to determine which fertilizers are significantly different from each other.

# Post-hoc test for one-way ANOVA
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.stats.multicomp import pairwise_tukeyhsd


# Create a dataframe
# Sample data: Growth of plants with three types of fertilizers
fertilizer1 = [20, 22, 19, 24, 25]
fertilizer2 = [28, 30, 27, 26, 29]
fertilizer3 = [18, 20, 22, 19, 24]

df = pd.DataFrame({"fertilizer": ["fertilizer1"] * 5 + ["fertilizer2"] * 5 + ["fertilizer3"] * 5,
                   "growth": fertilizer1 + fertilizer2 + fertilizer3})

# Perform Tukey's test
tukey = pairwise_tukeyhsd(endog=df["growth"], groups=df["fertilizer"], alpha=0.05)

# plot the results
tukey.plot_simultaneous()
# Print the results
print(tukey)

      Multiple Comparison of Means - Tukey HSD, FWER=0.05      
===============================================================
   group1      group2   meandiff p-adj   lower    upper  reject
---------------------------------------------------------------
fertilizer1 fertilizer2      6.0 0.0029   2.2523  9.7477   True
fertilizer1 fertilizer3     -1.4 0.5928  -5.1477  2.3477  False
fertilizer2 fertilizer3     -7.4 0.0005 -11.1477 -3.6523   True
---------------------------------------------------------------

7.4.8.3 Two-Way ANOVA in Python

Two-way ANOVA is used to compare two or more groups of samples across two continuous independent variables.

For example, you could use a two-way ANOVA to compare the height of people living in different cities and different age groups.

# Two-way ANOVA using statsmodels

import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

# Create a dataframe
# Sample data: Growth of plants with three types of fertilizers
fertilizer1 = [20, 22, 19, 24, 25]
fertilizer2 = [28, 30, 27, 26, 29]
fertilizer3 = [18, 20, 22, 19, 24]

df = pd.DataFrame({"fertilizer": ["fertilizer1"] * 5 + ["fertilizer2"] * 5 + ["fertilizer3"] * 5,
                   "growth": fertilizer1 + fertilizer2 + fertilizer3,
                   "age": [20, 22, 19, 24, 25] * 3})

# Fit the model
model = ols("growth ~ fertilizer * age", data=df).fit()

# Perform ANOVA and print the summary table
anova_table = sm.stats.anova_lm(model, typ=2)
print(anova_table)

# print the results based on if the p-value is less than 0.05
if anova_table["PR(>F)"][0] < 0.05:
    print(f"Reject null hypothesis: The means are not equal, as the p-value is less than 0.05")
else:
    print(f"Accept null hypothesis: The means are equal, as the p-value is greater than 0.05")

                    sum_sq   df          F    PR(>F)
fertilizer      154.533333  2.0  22.736922  0.000303
age              16.615385  1.0   4.889336  0.054340
fertilizer:age   12.000000  2.0   1.765594  0.225490
Residual         30.584615  9.0        NaN       NaN
Reject null hypothesis: The means are not equal, as the p-value is less than 0.05

/var/folders/4q/h5d6slgx2rs_drdwcmgf_htm0000gp/T/ipykernel_49854/2712025749.py:25: FutureWarning:

Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`

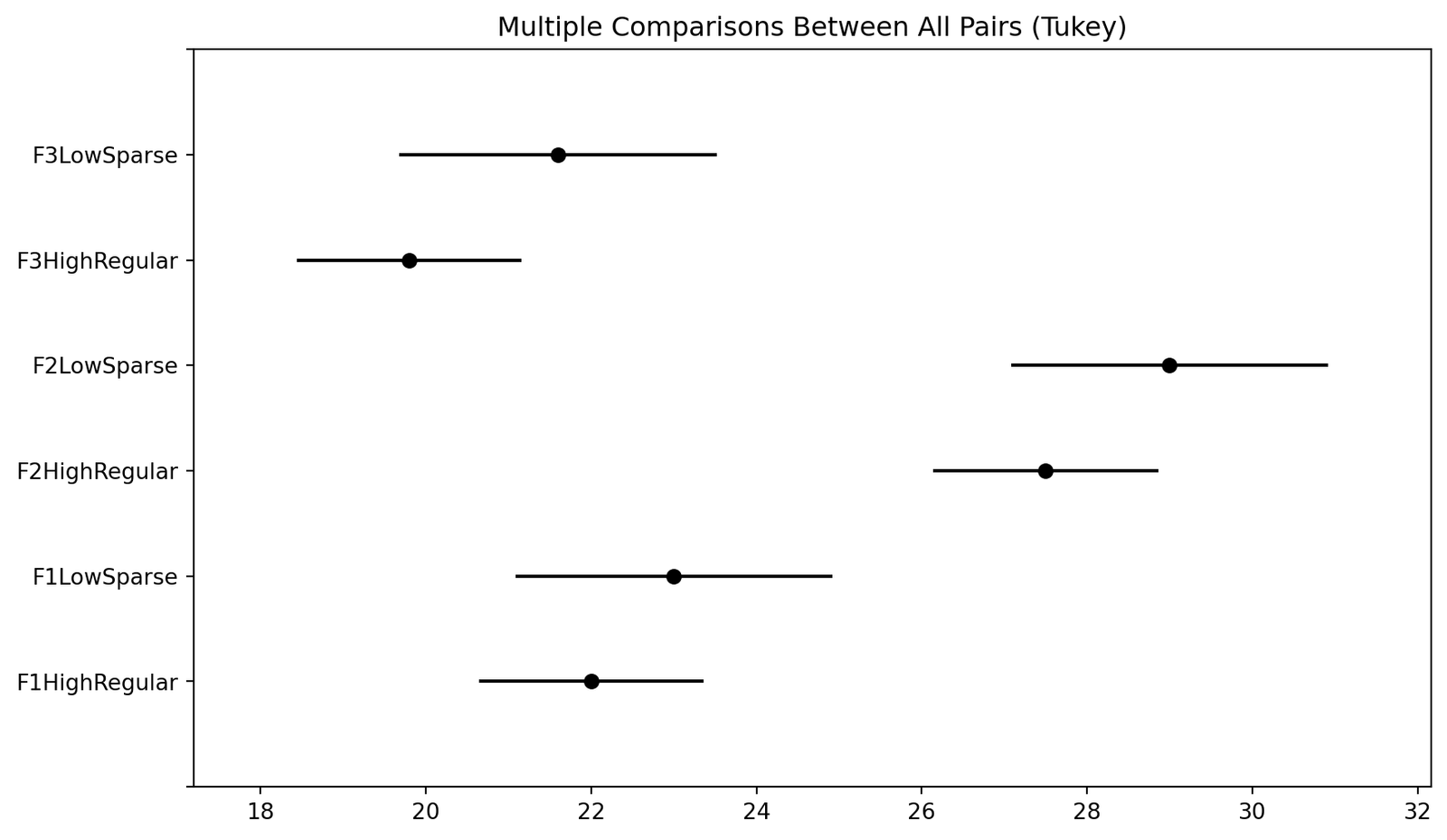
7.4.8.3.1 Post-Hoc Test for Two-Way ANOVA

We will perform a post-hoc test to determine which fertilizers are significantly different from each other.

# Post-hoc test for two-way ANOVA
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

# Sample data
data = pd.DataFrame({
    "Growth": [20, 22, 19, 24, 25, 28, 30, 27, 26, 29, 18, 20, 22, 19, 24,21, 23, 20, 25, 26, 29, 31, 28, 27, 30, 19, 21, 23, 20, 25],
    "Fertilizer": ["F1", "F1", "F1", "F1", "F1", "F2", "F2", "F2", "F2", "F2","F3", "F3", "F3", "F3", "F3", "F1", "F1", "F1", "F1", "F1","F2", "F2", "F2", "F2", "F2", "F3", "F3", "F3", "F3", "F3"],
    "Sunlight": ["High", "High", "High", "High", "High", "High", "High", "High", "High", "High","High", "High", "High", "High", "High", "Low", "Low", "Low", "Low", "Low","Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low"]
})

tukey = pairwise_tukeyhsd(data['Growth'], data['Fertilizer'] + data['Sunlight'], alpha=0.05)
# plot the results
tukey.plot_simultaneous()
print(tukey)

 Multiple Comparison of Means - Tukey HSD, FWER=0.05 
=====================================================
group1 group2 meandiff p-adj   lower    upper  reject
-----------------------------------------------------
F1High  F1Low      1.0 0.9786  -3.3434  5.3434  False
F1High F2High      6.0 0.0032   1.6566 10.3434   True
F1High  F2Low      7.0 0.0006   2.6566 11.3434   True
F1High F3High     -1.4 0.9145  -5.7434  2.9434  False
F1High  F3Low     -0.4 0.9997  -4.7434  3.9434  False
 F1Low F2High      5.0 0.0176   0.6566  9.3434   True
 F1Low  F2Low      6.0 0.0032   1.6566 10.3434   True
 F1Low F3High     -2.4 0.5396  -6.7434  1.9434  False
 F1Low  F3Low     -1.4 0.9145  -5.7434  2.9434  False
F2High  F2Low      1.0 0.9786  -3.3434  5.3434  False
F2High F3High     -7.4 0.0003 -11.7434 -3.0566   True
F2High  F3Low     -6.4 0.0016 -10.7434 -2.0566   True
 F2Low F3High     -8.4    0.0 -12.7434 -4.0566   True
 F2Low  F3Low     -7.4 0.0003 -11.7434 -3.0566   True
F3High  F3Low      1.0 0.9786  -3.3434  5.3434  False
-----------------------------------------------------

7.4.8.4 N-Way ANOVA or factorial ANOVA in Python

N Way ANOVA is used to compare N groups of samples across one continuous independent variables. In this example we will choose only 3 groups.

import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

# Sample data
data = pd.DataFrame({
    "Growth": [20, 22, 19, 24, 25, 28, 30, 27, 26, 29, 18, 20, 22, 19, 24,
               21, 23, 20, 25, 26, 29, 31, 28, 27, 30, 19, 21, 23, 20, 25,
               20, 22, 21, 23, 24, 26, 28, 25, 27, 29, 17, 19, 21, 18, 20],
    "Fertilizer": ["F1", "F1", "F1", "F1", "F1", "F2", "F2", "F2", "F2", "F2","F3", "F3", "F3", "F3", "F3", "F1", "F1", "F1", "F1", "F1","F2", "F2", "F2", "F2", "F2", "F3", "F3", "F3", "F3", "F3",
                   "F1", "F1", "F1", "F1", "F1", "F2", "F2", "F2", "F2", "F2", 
                   "F3", "F3", "F3", "F3", "F3"],
    "Sunlight": ["High", "High", "High", "High", "High", "High", "High", "High", "High", "High","High", "High", "High", "High", "High", "Low", "Low", "Low", "Low", "Low","Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low","High", "High", "High", "High", "High", "High", "High", "High", "High", "High", 
                 "High", "High", "High", "High", "High"],
    "Watering": ["Regular", "Regular", "Regular", "Regular", "Regular","Regular", "Regular", "Regular", "Regular", "Regular",
                 "Regular", "Regular", "Regular", "Regular", "Regular","Sparse", "Sparse", "Sparse", "Sparse", "Sparse", 
                 "Sparse", "Sparse", "Sparse", "Sparse", "Sparse",
                 "Sparse", "Sparse", "Sparse", "Sparse", "Sparse",
                 "Regular", "Regular", "Regular", "Regular", "Regular", 
                 "Regular", "Regular", "Regular", "Regular", "Regular",
                 "Regular", "Regular", "Regular", "Regular", "Regular"]
})

# Fit the model
model = ols('Growth ~ Fertilizer * Sunlight * Watering', data=data).fit()

# Perform three-way ANOVA
anova_results = sm.stats.anova_lm(model, typ=2)

print(anova_results)


# print the results based on if the p-value is less than 0.05

if anova_results["PR(>F)"][0] < 0.05:
    print("Reject null hypothesis: The means are not equal, as the p-value is less than 0.05")
else:
    print("Fail to reject null hypothesis: The means are equal, as the p-value is greater than 0.05")

                                    sum_sq    df             F        PR(>F)
Fertilizer                    6.023247e+02   2.0  7.466835e+01  4.618789e-14
Sunlight                      4.169869e-02   1.0  1.033852e-02  9.195328e-01
Watering                     -1.975467e+02   1.0 -4.897852e+01  1.000000e+00
Fertilizer:Sunlight           2.489798e-14   2.0  3.086527e-15  1.000000e+00
Fertilizer:Watering           2.816616e-01   2.0  3.491673e-02  9.657160e-01
Sunlight:Watering             2.054444e+01   1.0  5.093664e+00  2.969139e-02
Fertilizer:Sunlight:Watering  1.088889e+00   2.0  1.349862e-01  8.741344e-01
Residual                      1.573000e+02  39.0           NaN           NaN
Reject null hypothesis: The means are not equal, as the p-value is less than 0.05

/Users/aammar/Library/Python/3.9/lib/python/site-packages/statsmodels/base/model.py:1888: ValueWarning:

covariance of constraints does not have full rank. The number of constraints is 2, but rank is 1

/var/folders/4q/h5d6slgx2rs_drdwcmgf_htm0000gp/T/ipykernel_49854/1377226009.py:35: FutureWarning:

Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`

7.4.8.4.1 Post-Hoc Test for N-Way ANOVA

We will perform a post-hoc test to determine which Fertilizer * Sunlight * Watering interactions are significantly different from each other.

Code

from statsmodels.stats.multicomp import pairwise_tukeyhsd
# Sample data
data = pd.DataFrame({
    "Growth": [20, 22, 19, 24, 25, 28, 30, 27, 26, 29, 18, 20, 22, 19, 24,
               21, 23, 20, 25, 26, 29, 31, 28, 27, 30, 19, 21, 23, 20, 25,
               20, 22, 21, 23, 24, 26, 28, 25, 27, 29, 17, 19, 21, 18, 20],
    "Fertilizer": ["F1", "F1", "F1", "F1", "F1", "F2", "F2", "F2", "F2", "F2", 
                   "F3", "F3", "F3", "F3", "F3", "F1", "F1", "F1", "F1", "F1", 
                   "F2", "F2", "F2", "F2", "F2", "F3", "F3", "F3", "F3", "F3",
                   "F1", "F1", "F1", "F1", "F1", "F2", "F2", "F2", "F2", "F2", 
                   "F3", "F3", "F3", "F3", "F3"],
    "Sunlight": ["High", "High", "High", "High", "High", "High", "High", "High", "High", "High", 
                 "High", "High", "High", "High", "High", "Low", "Low", "Low", "Low", "Low", 
                 "Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low", "Low",
                 "High", "High", "High", "High", "High", "High", "High", "High", "High", "High", 
                 "High", "High", "High", "High", "High"],
    "Watering": ["Regular", "Regular", "Regular", "Regular", "Regular", 
                 "Regular", "Regular", "Regular", "Regular", "Regular",
                 "Regular", "Regular", "Regular", "Regular", "Regular",
                 "Sparse", "Sparse", "Sparse", "Sparse", "Sparse", 
                 "Sparse", "Sparse", "Sparse", "Sparse", "Sparse",
                 "Sparse", "Sparse", "Sparse", "Sparse", "Sparse",
                 "Regular", "Regular", "Regular", "Regular", "Regular", 
                 "Regular", "Regular", "Regular", "Regular", "Regular",
                 "Regular", "Regular", "Regular", "Regular", "Regular"]
})

tukey = pairwise_tukeyhsd(data['Growth'], data['Fertilizer'] + data['Sunlight'] + data['Watering'], alpha=0.05)
# plot the results
tukey.plot_simultaneous()
print(tukey)

        Multiple Comparison of Means - Tukey HSD, FWER=0.05        
===================================================================
    group1        group2    meandiff p-adj   lower    upper  reject
-------------------------------------------------------------------
F1HighRegular   F1LowSparse      1.0 0.9419  -2.2956  4.2956  False
F1HighRegular F2HighRegular      5.5    0.0   2.8092  8.1908   True
F1HighRegular   F2LowSparse      7.0    0.0   3.7044 10.2956   True
F1HighRegular F3HighRegular     -2.2 0.1647  -4.8908  0.4908  False
F1HighRegular   F3LowSparse     -0.4 0.9991  -3.6956  2.8956  False
  F1LowSparse F2HighRegular      4.5 0.0027   1.2044  7.7956   True
  F1LowSparse   F2LowSparse      6.0 0.0004   2.1946  9.8054   True
  F1LowSparse F3HighRegular     -3.2 0.0613  -6.4956  0.0956  False
  F1LowSparse   F3LowSparse     -1.4 0.8775  -5.2054  2.4054  False
F2HighRegular   F2LowSparse      1.5 0.7478  -1.7956  4.7956  False
F2HighRegular F3HighRegular     -7.7    0.0 -10.3908 -5.0092   True
F2HighRegular   F3LowSparse     -5.9 0.0001  -9.1956 -2.6044   True
  F2LowSparse F3HighRegular     -9.2    0.0 -12.4956 -5.9044   True
  F2LowSparse   F3LowSparse     -7.4    0.0 -11.2054 -3.5946   True
F3HighRegular   F3LowSparse      1.8 0.5804  -1.4956  5.0956  False
-------------------------------------------------------------------

7.4.9 Other types of POST-HOC tests

There are several post hoc tests used in statistics, each with its own strengths and weaknesses. Here’s a table summarizing some of the most common tests:

Post Hoc Test	Pros	Cons	Ideal Usage
Tukey’s HSD	- Controls Type I error well - Comparatively robust	- Can be conservative - Less powerful for unequal sample sizes	When equal sample sizes and normally distributed data are assumed.
Bonferroni	- Simple to compute - Very conservative	- Increases Type II errors - Can be too stringent for many comparisons	When few comparisons are made; useful in controlling Type I error in multiple testing.
Scheffé’s Test	- Flexible for any number of comparisons	- More conservative than others - Can be less powerful	When flexibility in hypothesis testing after ANOVA is needed; good for complex designs.
Dunn’s Test	- Suitable for non-parametric data	- Less powerful than parametric tests - Multiple comparison adjustments can be complex	When data do not meet parametric assumptions, particularly with Kruskal-Wallis test.
Holm’s Method	- Less conservative than Bonferroni - Controls Type I error well	- More complex calculation - Can still be conservative	When a balance between Type I error control and power is needed, especially with multiple comparisons.
Fisher’s LSD	- More powerful (higher chance to detect real differences)	- Higher risk of Type I error - Not recommended when there are many comparisons	When comparisons are planned and limited, often used in exploratory data analysis.
Ryan-Einot-Gabriel-Welsch Q (REGWQ)	- Controls the error rate well - Good for unequal sample sizes	- Complex calculation - Can be conservative	When there are unequal sample sizes, and control over Type I error is important.
Newman-Keuls	- More powerful for detecting differences	- Higher risk of Type I errors than other methods - Not recommended for many comparisons	When sample sizes are equal and the data are normally distributed; less used due to higher error risks.

7.4.9.0.1 Notes:

1. Choice of Test: The choice of post hoc test largely depends on the nature of your data, the number of comparisons, and the balance you want to strike between the risks of Type I and Type II errors.
2. Data Assumptions: Some tests assume normally distributed data and equal variances, while others are non-parametric and do not make these assumptions.
3. Type I and II Errors: There’s often a trade-off between the risk of Type I errors (false positives) and Type II errors (false negatives). More conservative tests (like Bonferroni) reduce the risk of Type I errors but increase the risk of Type II errors.

When conducting post hoc tests, it’s essential to understand these pros and cons to choose the most appropriate test for your specific statistical analysis.

7.4.10 MANOVA (Multivariate Analysis of Variance)

Manova is a multivariate extension of ANOVA. It is used to model two or more dependent variables that are continuous with one or more categorical predictor variables. It is often used to assess for differences between two or more groups.

To perform a Multivariate Analysis of Variance (MANOVA) in Python, we typically use the statsmodels library. MANOVA is used when there are two or more dependent variables and one or more independent variables. It tests whether the mean differences among groups on a combination of dependent variables are likely to have occurred by chance.

Here’s an example demonstrating how to create a MANOVA table in Python:

7.4.10.1 Example: MANOVA with StatsModels

Let’s say we have a dataset with two dependent variables (e.g., test scores in mathematics and science) and one independent variable (e.g., teaching method). We want to know if there are statistically significant differences in the dependent variables across the levels of the independent variable.

7.4.10.2 Explanation:

• Dataset Preparation: The data dictionary and DataFrame (df) contain the sample data. Replace this with your actual data.
• MANOVA Execution: The MANOVA.from_formula method is used to perform the MANOVA. The formula ‘MathScore + ScienceScore ~ Method’ indicates that MathScore and ScienceScore are dependent variables, and Method is the independent variable.
• Results: The mv_test() method is used to get the MANOVA test results, which are printed to the console.

This script will output the MANOVA table, including Pillai’s trace, Wilks’ lambda, Hotelling-Lawley trace, and Roy’s greatest root test statistics, along with their associated F-values, degrees of freedom, and p-values. These results will help you determine if there are statistically significant differences in the dependent variables across the levels of the independent variable.

# Import the required libraries
import pandas as pd
from statsmodels.multivariate.manova import MANOVA

# Create a sample dataset
data = {
    'Method': ['A', 'A', 'A', 'B', 'B', 'B', 'C', 'C', 'C'],
    'MathScore': [20, 22, 21, 19, 18, 20, 22, 23, 21],
    'ScienceScore': [30, 28, 29, 33, 32, 31, 29, 27, 28]
}

df = pd.DataFrame(data)

# Perform the MANOVA
maov = MANOVA.from_formula('MathScore + ScienceScore ~ Method', data=df)
print(maov.mv_test())

                   Multivariate linear model
================================================================
                                                                
----------------------------------------------------------------
       Intercept          Value   Num DF Den DF  F Value  Pr > F
----------------------------------------------------------------
          Wilks' lambda    0.0005 2.0000 5.0000 4711.5000 0.0000
         Pillai's trace    0.9995 2.0000 5.0000 4711.5000 0.0000
 Hotelling-Lawley trace 1884.6000 2.0000 5.0000 4711.5000 0.0000
    Roy's greatest root 1884.6000 2.0000 5.0000 4711.5000 0.0000
----------------------------------------------------------------
                                                                
----------------------------------------------------------------
             Method         Value  Num DF  Den DF F Value Pr > F
----------------------------------------------------------------
              Wilks' lambda 0.1802 4.0000 10.0000  3.3896 0.0534
             Pillai's trace 0.8468 4.0000 12.0000  2.2031 0.1301
     Hotelling-Lawley trace 4.4000 4.0000  5.1429  5.4000 0.0444
        Roy's greatest root 4.3656 2.0000  6.0000 13.0969 0.0065
================================================================

7.4.10.3 Interpertation of MANOVA Results

The MANOVA results provided contain two main parts: the test statistics associated with the intercept and the test statistics associated with the independent variable (Method). Each part includes four different test statistics: Wilks’ lambda, Pillai’s trace, Hotelling-Lawley trace, and Roy’s greatest root. Let’s interpret these results:

7.4.10.3.1 Intercept Part

1. Wilks’ Lambda: A value close to 0 (0.0005) with a significant F-value (4711.5) and a p-value of 0.0000 indicates that the model with the intercept is significantly different from a model without the intercept.
2. Pillai’s Trace: Similar to Wilks’ lambda, a value close to 1 (0.9995) with a significant F-value and p-value indicates strong model significance.
3. Hotelling-Lawley Trace: A very high value (1884.6) with a significant F-value and p-value also suggests strong model significance.
4. Roy’s Greatest Root: Like Hotelling-Lawley trace, a high value (1884.6) with a significant F-value and p-value indicates the model’s significance.

7.4.10.3.2 Method Part

1. Wilks’ Lambda: A value of 0.1802 with an F-value of 3.3896 and a p-value of 0.0534. This p-value is marginally above the typical alpha level of 0.05, suggesting that the differences in group means are not quite statistically significant at the 5% level.
2. Pillai’s Trace: A value of 0.8468, F-value of 2.2031, and a p-value of 0.1301. This result further indicates that the group means are not significantly different, as the p-value is above 0.05.
3. Hotelling-Lawley Trace: A value of 4.4 with an F-value of 5.4 and a p-value of 0.0444. This p-value is below 0.05, indicating significant differences in the group means.
4. Roy’s Greatest Root: A value of 4.3656, with an F-value of 13.0969 and a p-value of 0.0065. This result suggests significant differences in the group means, as indicated by this low p-value.

7.4.10.3.3 Overall Interpretation

• The significant intercept part indicates that the overall model is significant.
• For the Method part, different test statistics provide somewhat conflicting results. Wilks’ Lambda and Pillai’s Trace suggest that the means of different methods are not significantly different, while Hotelling-Lawley Trace and Roy’s Greatest Root suggest significant differences.
• Such discrepancies can occur due to the sensitivity of each test to different assumptions and data characteristics. In practice, when results conflict, it’s often advisable to further investigate the data, potentially considering other forms of analysis or looking into specific pairwise comparisons for more insights.

7.4.11 Correlation

Pearson correlation, statistics mein istemal hone wala aik measure hai jo do variables ke darmiyan linear relationship ko measure karta hai.

Types of Correlation tests:

• Pearson’s correlation coefficient
• Spearman’s rank correlation coefficient
• Kendall’s rank correlation coefficient
• Point-Biserial correlation coefficient
• Biserial correlation coefficient
• Phi coefficient
• Cramer’s V

7.4.11.1 Pearson’s correlation coefficient

Pearson’s correlation coefficient is a measure of the linear correlation between two variables X and Y. It has a value between +1 and −1, where 1 is total positive linear correlation, 0 is no linear correlation, and −1 is total negative linear correlation.

\[r_{xy} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}}\]

7.4.11.2 Spearman’s rank correlation coefficient

Spearman’s rank correlation coefficient is a nonparametric measure of the monotonicity of the relationship between two datasets. Unlike the Pearson correlation, the Spearman correlation does not assume that both datasets are normally distributed. Like other correlation coefficients, this one varies between +1 and −1 with 0 implying no correlation. Correlations of −1 or +1 imply an exact monotonic relationship. Positive correlations imply that as x increases, so does y. Negative correlations imply that as x increases, y decreases.

\[r_s = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}}\]

7.4.11.3 Pearson’s and Spearman’s correlation in Python

There are many ways to calculate Pearson’s correlation coefficient in Python. Here’s are all the examples, one by one:

1. By defining function

You can unfold the codes by clicking on the arrow on the left side of the code.

Code

# pearson's correlation coefficient
import pandas as pd
import numpy as np
def pearson(x, y):
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    x_std = np.std(x)
    y_std = np.std(y)
    n = len(x)
    return sum((x-x_mean)*(y-y_mean))/(n*x_std*y_std)
# example dataset
x = np.array([1,2,3,4,5])
y = np.array([2,4,5,4,5])
print(f"Pearson Correlation Coefficient: {pearson(x,y)}")

# print with if else statement 
if pearson(x,y) < 0.6 > 0:
    print("Positive Correlation.")
elif pearson(x,y) > 0.6:
    print("Highly Positive Correlation.")
elif pearson(x,y) > -0.6 < 0:
    print("Negative Correlation.")
elif pearson(x,y) < -0.6:
    print("Highly Negative Correlation.")
else:
    print("No Correlation.")

Pearson Correlation Coefficient: 0.7745966692414834
Highly Positive Correlation.

Code

import pandas as pd
import numpy as np

# example dataset
x = np.array([1,2,3,4,5])
y = np.array([2,4,5,4,5])

def pearson(x, y):
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    x_std = np.std(x)
    y_std = np.std(y)
    n = len(x)
    return sum((x-x_mean)*(y-y_mean))/(n*x_std*y_std)

# Spearman's correlation coefficient
def spearman(x, y):
    x_rank = pd.Series(x).rank()
    y_rank = pd.Series(y).rank()
    return pearson(x_rank, y_rank)

print(f"Spearman Correlation Coefficient: {spearman(x,y)}")

# print with if else statement
if spearman(x,y) < 0.6 > 0:
    print("Positive Correlation")
elif spearman(x,y) > 0.6:
    print("Highly Positive Correlation")
elif spearman(x,y) > -0.6 < 0:
    print("Negative Correlation")
elif spearman(x,y) < -0.6:
    print("Highly Negative Correlation")
else:
    print("No Correlation")

Spearman Correlation Coefficient: 0.7378647873726218
Highly Positive Correlation

2. Using numpy

Code

import pandas as pd
import numpy as np  

# example dataset
x = np.array([1,2,3,4,5])
y = np.array([2,4,5,4,5])

# pearson's correlation coefficient

pearson = np.corrcoef(x,y)
print(f"Pearson Correlation Coefficient: {pearson[0,1]}")

Pearson Correlation Coefficient: 0.7745966692414834

3. Using Pandas on series

Code

# creata an example dataset

x = pd.Series([1,2,3,4,5])
y = pd.Series([2,4,5,4,5])

# pearson's correlation coefficient
pearson_corr = x.corr(y)
print(f"Pearson Correlation Coefficient: {pearson_corr}")

Pearson Correlation Coefficient: 0.7745966692414834

4. Using Pandas on dataframe

Code

df = pd.DataFrame({'x':x, 'y':y})

# pearson's correlation coefficient
pearson_corr = df.corr(method = 'pearson')
spearman_corr = df.corr(method = 'spearman')

print(f"Pearson Correlation Coefficient:\n {pearson_corr}")
print("====================================")
print(f"Spearman Correlation Coefficient:\n {spearman_corr}")

Pearson Correlation Coefficient:
           x         y
x  1.000000  0.774597
y  0.774597  1.000000
====================================
Spearman Correlation Coefficient:
           x         y
x  1.000000  0.737865
y  0.737865  1.000000

---

7.5 Follow us

Follow us

Main umeed karta hun k ap ko ye chapter ne bht kuch seekhaya ho ga, or agar sach main seekhaya hy then please do support us by sharing this book with your friends and colleagues. Also, do share your feedback with us, so that we can improve our work in future.

---