Standard Deviation: The Gateway to Understanding Data Variability 📊🔍
Welcome to the World of Standard Deviation!
In the intricate tapestry of statistics, understanding the variability or spread of data is as crucial as knowing its average. Standard deviation, a key statistical tool, provides profound insights into this variability, helping us comprehend the consistency and predictability of data. Let’s dive into the nuances of standard deviation, exploring its meaning, calculation, and real-world applications. 🚀
What is Standard Deviation? 🤔
Standard deviation is a measure that quantifies the amount of variation or dispersion in a set of data values. It’s akin to assessing the roughness or smoothness of a terrain in geography. A low standard deviation means that the data points are close to the mean, indicating smooth and consistent terrain. In contrast, a high standard deviation indicates that the data points are spread out over a wider range of values, akin to a rough, uneven landscape.
The Calculation: Cracking the Code of Variability 🧮
Standard deviation is the square root of the variance. For a set of data, it’s calculated using the following formulas:
- Population Standard Deviation
\[ \sigma = \sqrt{\frac{\sum (x_i – \mu)^2}{N}} \] - Sample Standard Deviation
\[ s = \sqrt{\frac{\sum (x_i – \bar{x})^2}{n – 1}} \]
Where \( x_i \) represents each data point, \( \mu \) is the population mean, \( \bar{x} \) is the sample mean, and \( N \) and \( n \) are the number of data points in the population and sample, respectively.
let’s go through an example to calculate the standard deviation of a sample dataset. Suppose we have the following set of data, representing, for instance, the scores of students on a test: [85, 90, 78, 88, 95].
Steps to Calculate the Sample Standard Deviation:
Calculate the Mean (Average):
First, find the mean of the dataset.
\[ \text{Mean} = \frac{\text{Sum of all scores}}{\text{Number of scores}} = \frac{85 + 90 + 78 + 88 + 95}{5} = \frac{436}{5} = 87.2 \]Subtract the Mean and Square the Result: Next, subtract the mean from each score and square the result.
Calculate the Average of These Squared Differences: Now, sum up these squared differences and divide by the number of data points minus one (since this is a sample standard deviation).
Take the Square Root of the Variance: Finally, take the square root of the variance to get the standard deviation.
\[ \text{Standard Deviation} = \sqrt{39.7} \approx 6.3 \]
Result:
The standard deviation of the students’ scores is approximately 6.3. This value tells us how much the scores typically deviate from the mean score of the students. A smaller standard deviation would indicate that the scores are more closely clustered around the mean, while a larger one would suggest a wider spread of scores.
Standard Deviation in Python
Here is the python code:
import numpy as np
# Example dataset
data = [85, 90, 78, 88, 95]
# Calculate the standard deviation
std_dev = np.std(data, ddof=1) # 'ddof=1' means Delta Degrees of Freedom = 1 for sample standard deviation
print(f"The standard deviation of the dataset is: {std_dev}")
The standard deviation of the dataset is: 6.300793600809346
Real-Life Example: 🏫
Consider a school where we want to understand the consistency of students’ test scores. The standard deviation of these scores will show how much the students’ performances vary from the average performance.
The Significance of Standard Deviation in Data Analysis 🌟
- Assessing Data Spread: Standard deviation provides insights into how spread out the data is, which is crucial for understanding the reliability and quality of the data.
- Basis for Further Statistical Analysis: It’s a foundational component for many statistical procedures, including hypothesis testing and confidence intervals.
- Comparative Analysis: Standard deviation allows for comparing the variability of different datasets, even if their means are different.
Standard Deviation in Everyday Life: Practical Applications 🌍
- In Finance and Investment: Investors use standard deviation to measure the volatility of stock prices or investment returns, helping them understand the risk involved.
- In Quality Control: Manufacturers analyze the standard deviation in product dimensions or weights to ensure consistency and quality in production.
- In Sports and Performance Analysis: Coaches and analysts use standard deviation to evaluate the consistency of an athlete’s performance.
Visualizing Standard Deviation: Beyond the Numbers 📊
Graphical tools like bell curves and scatter plots, enriched with standard deviation, transform abstract statistical concepts into visually intuitive formats. This enhances understanding and aids in decision-making.
import matplotlib.pyplot as plt
import numpy as np
# Example data
categories = ['Category A', 'Category B', 'Category C']
values = [20, 35, 30]
std_devs = [2, 3, 4]
# Creating the bar plot
plt.figure(figsize=(8, 6))
bar_positions = np.arange(len(categories))
plt.bar(bar_positions, values, yerr=std_devs, capsize=5, color='skyblue', alpha=0.7)
# Adding labels and title
plt.xlabel('Categories')
plt.ylabel('Values')
plt.xticks(bar_positions, categories)
plt.title('Bar Plot with Standard Deviation')
# Show the plot
plt.show()
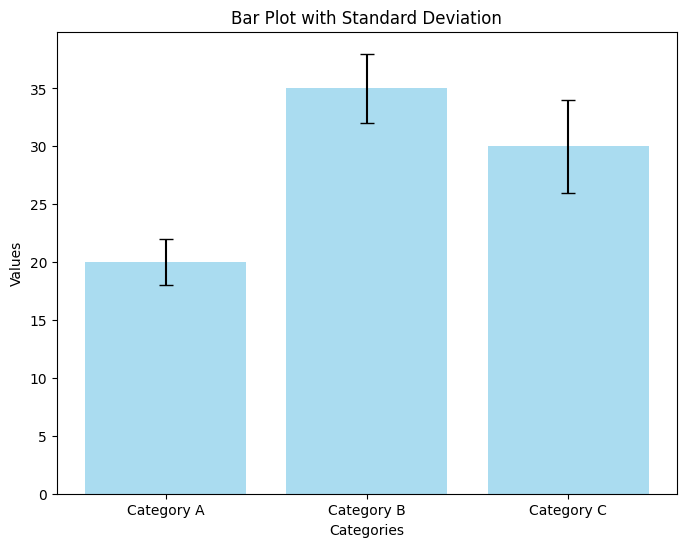
Here’s a bar plot illustrating values for different categories along with their respective standard deviations:
- Bar Representation: Each bar represents the value for a specific category (Category A, B, and C).
- Standard Deviation: The error bars (vertical lines on top of each bar) indicate the standard deviation for each category. These error bars give a visual sense of the variability or spread of the data around the mean value for each category.
- Capsize: The horizontal lines at the top of each error bar (known as caps) help in clearly demarcating the range of the standard deviation.
This type of plot is particularly useful for visually comparing the mean values across different categories while also providing an immediate sense of the variability within each category.
Beyond Standard Deviation: The Broader Context 🌈
While standard deviation is a powerful tool, it’s part of a larger statistical toolkit. Understanding its relationship with other measures like mean and variance provides a more comprehensive view of the data.
Conclusion: Embracing the Predictability in Variability 🚀
Standard deviation is not just a statistical measure; it’s a key to unlocking the secrets of data variability. It enables us to appreciate the predictability and consistency hidden within datasets. As you journey through the realm of data analysis, let standard deviation be your guide to understanding the fascinating world of data variability.











Fantastic site. Lots of helpful information here. I am sending it to some friends ans additionally sharing in delicious. And of course, thanks for your effort!
I assumed after reading and watching the topics of variability:
1. A range represents a broad overview of data
2. IQR is the shortest form of range
3. Variance is the shortest form of IQR
4. Standard Deviation is the shortest form of Variance
5. Standard Error is the shortest form of Standard Deviation
Informative and useful blog.
Done
AOA, This statistics blog post on “Standard Deviation” provides a clear and concise explanation of the concept. It effectively communicates the meaning, calculation, and real-world applications of standard deviation. The inclusion of examples and Python code enhances the understanding of the topic. It is an informative and well-written blog post for anyone interested in learning about standard deviation. ALLAH PAK ap ko dono jahan ki bhalian aata kry AAMEEN.